(圆锥曲线的几何性质)抛物线（1）

(圆锥曲线的几何性质)抛物线（1）

从今天开始，老鼠会陆续地发一些《圆锥曲线的几何性质》里的题。这是一本不错的书，作者科克肖特另辟蹊径，用纯几何的方法系统地描述了圆锥曲线。这本书很早以前的，所以有许多调和性质没有探索。

里面命题的证明老鼠就不多说了，读者可以参照“pdcxs”大神的视频（老鼠不会做视频，只能写文章啦，嘤嘤嘤）。废话不多说，现在就开始吧！

定义：抛物线是到一个定点的距离等于到一条定直线的距离的点的轨迹。其中，定点叫做焦点，通常记作S，定直线叫做准线，通常记作I。

定义：（也算是一道命题）抛物线是轴对称曲线，我们将对称轴简称为轴。定义：轴与抛物线的交点叫做抛物线的顶点，通常记作A。

大概长这样

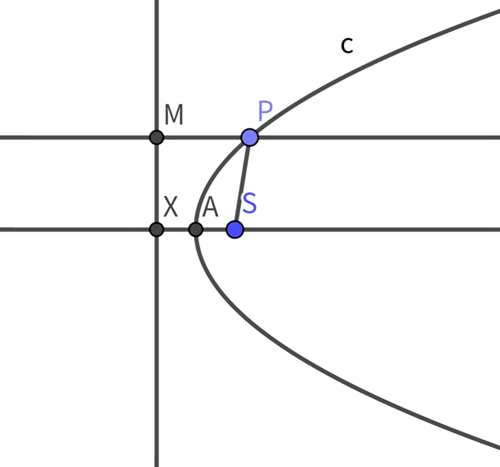
P是曲线上任意一点

命题1：做出抛物线上的点，并且过焦点做准线的垂线是抛物线的轴。

主要来看习题（注意：粉色标注的字母都是常用字母，请多加牢记）：

1.做出抛物线上的点

2.P、Q是抛物线上任意两点，P、Q是P、Q关于轴的对称点，则PQ，PQ和轴三线共点

3.P做准线的垂线叫准线与M，过A平行于准线的直线交SM于Y，则SM被Y点平分

4.在三的基础上求证PY垂直于SM，且PY平分∠SPM

5.作SZ垂直于SP交准线于Z，则PZ平分∠SPM

6.过焦点的两条弦叫做焦点弦，若两条焦点弦相等，则它们的中点的连线垂直于轴

7.设动圆与定直线相切，且经过一定点，求圆心的轨迹

8.设动圆与一定圆和一定直线同时相切，求圆心轨迹

9.平行于轴的直线，与抛物线只有一个交点

读者可以想想再看答案哟！

1.参照命题1

2.由题意知，轴是PP的中垂线，也是QQ的中垂线，所以PQQP是等腰梯形，显然PQ与PQ的交点在轴上

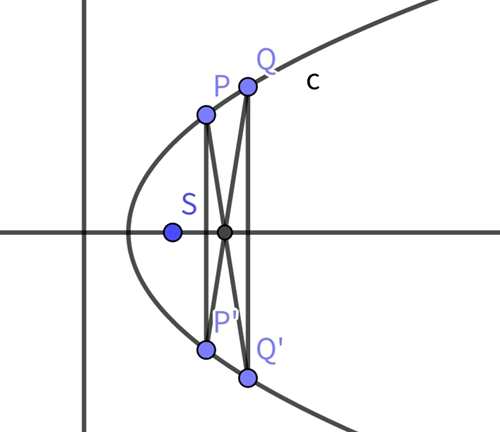
第二题图

3.设轴交准线与X，AY交PM于C，很容易看出CM=AX=AS，于是我们可以证ΔYCM≌ΔYAS（AAS），最后我们得到了YM=YS

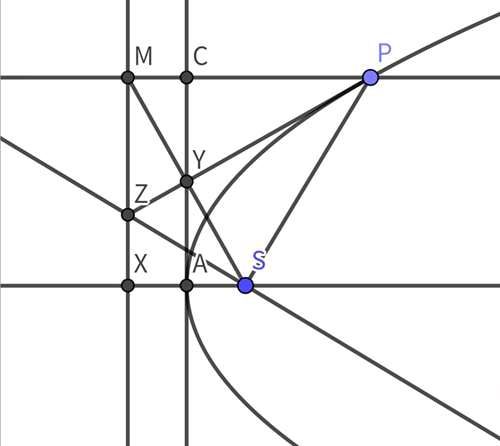
3、4、5题图

4.用上习题3的结论，再加上抛物线定义PM=PS，三线合一，得到PY平分∠SPM

5.参照命题5（估计就是下下下下一期吧）

6.（这题感谢pdcxs大佬）我们设焦点弦分别为PP和QQ，中点分别为I和H，我们再过H、I、Q、Q作准线的垂线，垂足为C、D、E、F。首先EQ=SQ，FQ=SQ，所以QQ=EQ+FQ，由梯形的中位线得CH=½QQ，同理DI=½PP，于是CH平行且相等DI，所以四边形CDIH是平行四边形，IH平行准线，而准线垂直于轴，所以IH垂直于轴。这里其实还能发现一个小推论：若PP、QQ是焦点弦，那么PQPQ是梯形的充要条件是PP=QQ

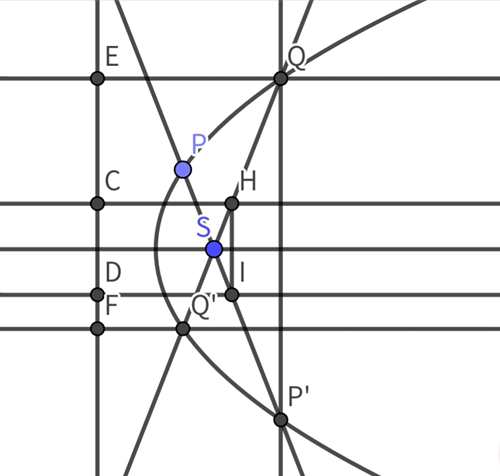
得到大佬提醒的我

7.设定点为C，定直线为l，动圆圆心为F。根据抛物线的定义，FC=FG，可以说明F的轨迹是抛物线。进一步，我们还发现F在CG的中垂线上。

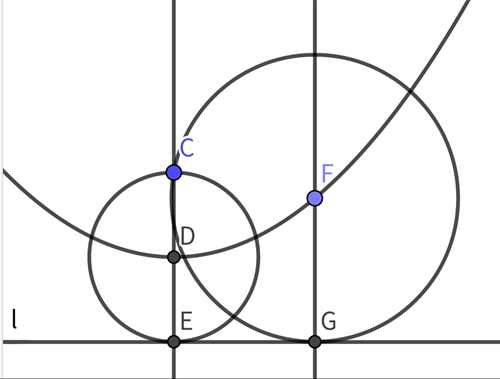
第7题

8.借助第7题的结论，作k平行于l，且k和l的距离等于CD，我们会发现，圆心轨迹是以C为焦点，k为准线的抛物线。同理圆心在CL的中垂线上。

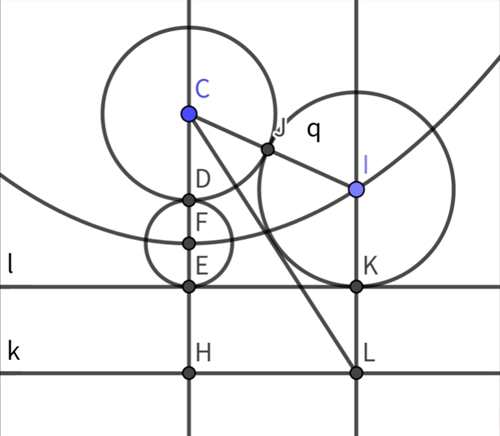
第8题

9.这题怎么说呢，上过初中的都知道怎么做吧，不就是个二次函数么，不过为了体现我们的几何精神，还是解释一下吧。反证法：设有两个交点P、Q，则有PM=SP=SQ=QM，但这是不可能的，所以只有一个交点。（因为没办法画图，所以老鼠就拍了几张《圆锥曲线论》的图片）

老鼠又来推销书了

拿图片H2O文章

上面也说了，可能会有下期，但也只是可能，假如没人来看，没人点赞，没人投币（这个算了），老鼠也没有动力继续写下去呀！所以就靠大家了！谢谢观看！

以上就是（(圆锥曲线的几何性质)抛物线（1））全部内容，收藏起来下次访问不迷路！