三角形四心随想 (三角形四心与向量的关系)
三角形四心随想 (三角形四心与向量的关系)
四心虽然算是三角形中很基础的四个点,但它们所牵扯的定理也是最多的,咱们先来一个个了解一下吧。什么?上小学就都学过了?那我还怎么水……写下面的内容啊?算了,你们看看就好|・ω・`)
首先是重心(Barycenter),它是三角形三条基础线——中线的交点:
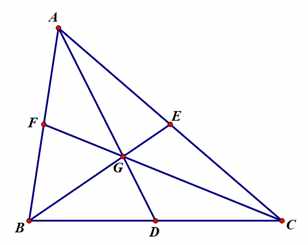
重心通常以字母G标注
而三条中线交于一点的规律又被称为“重心定理”,咱们来简单的证明一下:
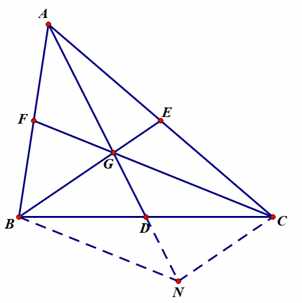
如图:
连接中线BE与CF,两线相交于点G,连接AG并延长至点N,使AG=GN,连接BN,CN;
∵F为AB的中点,G为AN的中点
∴FG为△ABN的中位线
∴FG∥BN
同理可得:EG∥CN
∴四边形BGCN为平行四边形
∴BC与GN互相平分,即D点为BC的中点
∴AD也是△ABC的中线
得证
接下来是外心(Circumcenter)——三条中垂线的交点:
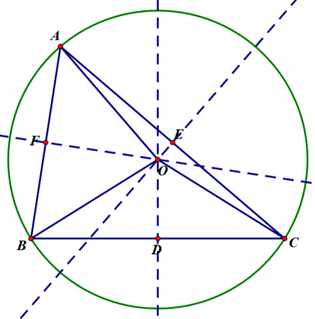
外心通常用字母O标注
至于“外心定理”:三角形的三条中垂线相交于一点,我们只需要一个小引理就可以证明了。
中垂线定理及其逆定理:一条线段的中垂线上的点,到这条线段两端点的距离相等;反过来说,到某条线段两端点距离相等的点,一定在这条线段的中垂线上。
上面这条引理的证明可以利用全等三角形SAS:
其逆定理就用直角三角形全等HL证明
了解了这条引理后,很容易就能证明OA=OB=OC,从而O点在三条边的中垂线上,三线共点证毕。同时,通过OA=OB=OC,我们可以以O点为圆心,OA为半径画圆,易知A,B,C均在⊙O上,即⊙O外接于△ABC,⊙O是△ABC的外接圆,“外心(外接圆圆心)”这一名称由此而来。
再接下来就是内心(Incenter)了——三条角平分线的交点:
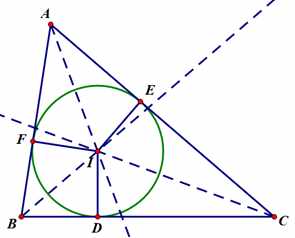
内心通常用字母I标注
证明“内心定理”与证明“外心定理”方法一样,也只需要一个引理就可以证明三角形的三条角平分线相交于一点。
角平分线性质定理及逆定理:角平分线上任意一点到角两边的距离相等,到角两边距离相等的点就在角平分线上。
引理的证明方法是利用全等三角形ASA:
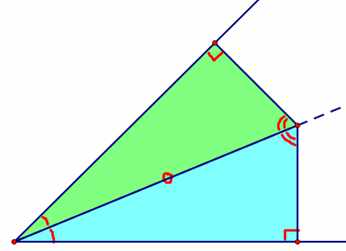
其逆定理也是用全等直角三角形HL证明
通过引理我们很简单就可得到上图中:ID=IE=IF,即D,E,F在以I点为圆心的圆上,同时⊙I与AB,BC,CA相切,即⊙I内切于△ABC,“内心(内切圆圆心)”由此而来。
最后就是我们的第四个心——垂心(Ortho-center),三条高线的交点:
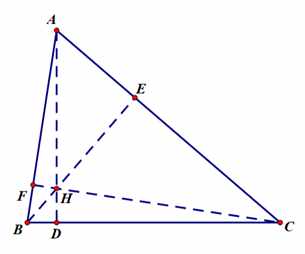
垂心通常用字母H标注
“垂心定理”,三条高线相交于一点的证明要用到四点共圆的性质,相信大家都有所了解吧,在此我就直接给出证法吧:
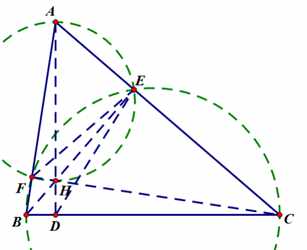
如图:
作BE⊥AC,CF⊥AB,BE与CF相交于点H,连接AH并延长,交BC于点D,连接FE与DE
由条件可知:∠BFC=∠BEC=90°,同时∠AFH=∠AEH=90°
∴B,F,E,C四点共圆,A,F,H,E也四点共圆
∴∠FCD=∠FCB=∠FEB=∠FEH=∠FAH=∠FAD
∴F,A,C,D四点共圆
∴∠ADC=∠AFC=90°
∴AD⊥BC
∴AD也是△ABC的一条高
三线共点证毕
好了,三角形的四心都一一介绍完毕了。什么?少了旁心?由于它涉及外角平分线,而且还是“三位一体”,所以这次我们就先不介绍它了吧,留到后面再说,让我们先来看看基础四心之间有些什么有趣的联系吧。
欧拉线:
大家应该都知道,过两点可做一条直线,毕竟这可是欧氏几何的公设一啊,所以如果我们再加上一个点,用三个点为基础作线,一般可以得到三条互不重合的直线,但是,万事都有例外,这三条线可以如同三角形三条边一样不重合,也可以相互重合成为一条直线,即“三点共线”,而三角形的四心在不重合的情况下可是有四个点的啊,按理来说应该可以画出4C2=6条不同的直线。但是,就在这四个点中,“例外”出现了:外心O,重心G,垂心H,这三个点在任意三角形中,都在一条直线上,而这条线,就是接下来要说的:欧拉线。
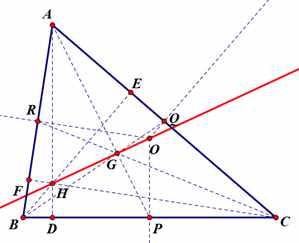
图中的红线就是欧拉线
我找了个奇妙的方法证明这个三点共线:
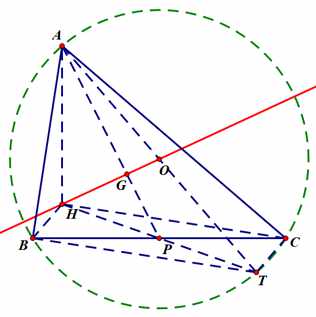
如图:做出△ABC的外接圆⊙O,延长AO交⊙O于点T,得到直径AT,连接TB,TH,TC
∵AT为直径
∴∠ABT=∠ACT=90°
∴TB⊥AB,TC⊥AC
又∵CH⊥AB,BH⊥AC
∴CH∥TB,BH∥TC
∴四边形HBTC为平行四边形
∴BC与TH相互平分,即点P既是BC的中点,也是TH的中点
∴AP既是△ABC的一条中线,也是△AHT的一条中线
而HO显然也是△AHT的一条中线
∴HO与AP的交点点G就是△AHT的重心
接下来我们要用到重心的一个性质:重心到顶点的距离是它到对边中点距离的2倍,这个性质的证明我就不写了,咱们直接用吧
∵G为△ABC的重心,G为△AHT的重心,而AP同为两三角形的中线
∴G与G都在AP上
又由重心的性质,得:AG:GP=AG:GP=2
∴G与G重合
而G在△AHT的中线HO上
∴H,G,O三点共线
证毕
同时我们还能得到:HG:GO=2
四心共点:
上面我们证明了,外心O,重心G,垂心H三点一定是共线的,那有没有四点共线的情况呢?当然有了,这个问题简单到让你们怀疑我在凑字数了吧。等腰三角形由于“三线合一”,显而易见的能使四心共线。那么,让我们将问题反过来提:如何证明四心共线的三角形就是等腰三角形?或者这么问:内心在欧拉线上的三角形是等腰三角形吗?
我想,大部分人肯定想的是:“这个逆命题不和正命题一样简单吗?只要用‘三线合一’逆推一下不就出来了吗?”
欸,这个逻辑还真不能这么想,因为欧拉线可不一定过三角形的顶点哦,而“三线合一”指的是中线,角平分线,高线的重合,前提是从同一顶点引出的,而现在,虽然有一条欧拉线,但是没有证明这条线是否是中线,角平分线或高线中的任意一条,如何能动用“三线合一”去逆推呢?
所以,想用“三线合一”,就得先证明三角形的内心在欧拉线上时,欧拉线过三角形的其中一个顶点,然后才能逆推出等腰三角形哦。
不过,有一种证明方法不用使用“三线合一”去逆推,也能完成证明,且听我一一道来:
首先,让我们从一般的三角形中找一些普遍的边角关系吧
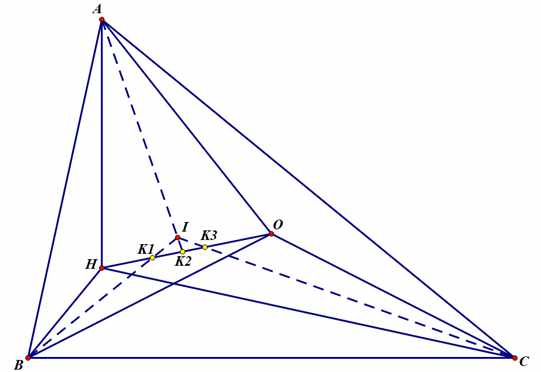
注意K1,K2,K3哦
∵∠HAB=90°-∠B=∠HCB,而∠AOC=2∠B,且OA=OC
∴∠OAC=∠OCA=90°-∠B=∠HAB=∠HCB
同理:
∠OBC=∠OCB=∠HBA=∠HCA
∠OAB=∠OBA=∠HAC=∠HBC
而AI,BI,CI分别为∠A,∠B,∠C的角平分线
∴∠IAB=∠IAC,∠IBA=∠IBC,∠ICA=∠ICB
∴∠IAH=∠IAB-∠HAB=∠IAC-∠OAC=∠IAO
同理:∠IBH=∠IBO,∠ICH=∠ICO
即AI,BI,CI也分别是∠OAH,∠OBH,∠OCH的角平分线
由角平分线定理,可得:
AH:AO=K2H:K2O
BH:BO=K1H:K1O
CH:CO=K3H:K3O
当内心I不在OH上时,显然K1,K2,K3在OH的不同位置
从而:K1H:K1O≠K2H:K2O≠K3H:K3O
∴AH:AO≠BH:BO≠CH:CO
同时AO=BO=CO
∴AH≠BH≠CH
但接下来,当点I在OH上时(如图):
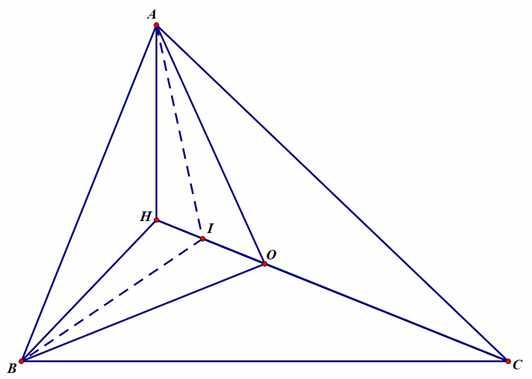
K1,K2,K3不见了
显然,在这种情况下,K1,K2与I重合了,至于K3,我们不好确定它的位置,就不显示了。
由上面的等式关系,我们依然能够得到:
AH:AO=K2H:K2O
BH:BO=K1H:K1O
但由于K1,K2与I重合,于是我们就可以将等式改成:
AH:AO=IH:IO=BH:BO
∵AO=BO
∴AH=BH
∴∠HAB=∠HBA
而通过上面我们已知:
∠HAB=∠HCB,∠HBA=∠HCA
∴∠HCB=∠HCA
∴CH就是∠ACB的角平分线
∴I就在CH上,即H,I,C三点共线
同时,O也与H,I共线
∴H,I,O,C都在一条直线上
∵HA=HB,OA=OB
由前面中垂线的逆定理可知:
H,O均在线段AB的中垂线上
而C与HO共线
∴C也在AB的中垂线上
∴CA=CB
∴H,I,O三点共线的△ABC是等腰三角形
而通过欧拉线可知,重心G也在直线HO上
∴四心共线的三角形就是等腰三角形
证毕
当然,除了K1,K2的重合,K1,K2,K3不管是哪两点重合,最后都可以推出原三角形是等腰三角形。
不过,我好像跑题了欸,明明这一段是要讲“四心共点”的,怎么成了四心共线了?不急,有了四心共线做的铺垫,咱们就可以轻松理解四心共点了嘛。
首先,由上面的“四心共线”可知,这条线一定会经过三角形的一个顶点,且这个顶点所在的角就是等腰三角形的顶角,而当“四心共点”时,显然其符合“四心共线”的条件,那么这条线过了三角形的哪个顶点呢?是不是从任一顶点引出的线都可使四心在这条线上?所以这个三角形的任意一个角都可以作为等腰三角形的顶角,也可以作为其底角,所以三个角相等,三条边相等,这是个等边三角形。这逻辑是不是完全没问题(ಡωಡ)
不过,除了上面这个“奇葩”的逻辑之外,我们可以“正经”的将:“四心共点的三角形就是等边三角形”再证明一遍,同时,我还可以将“四心共点”改成“二心共点”,结果不变,所以,就有如下六种情况:
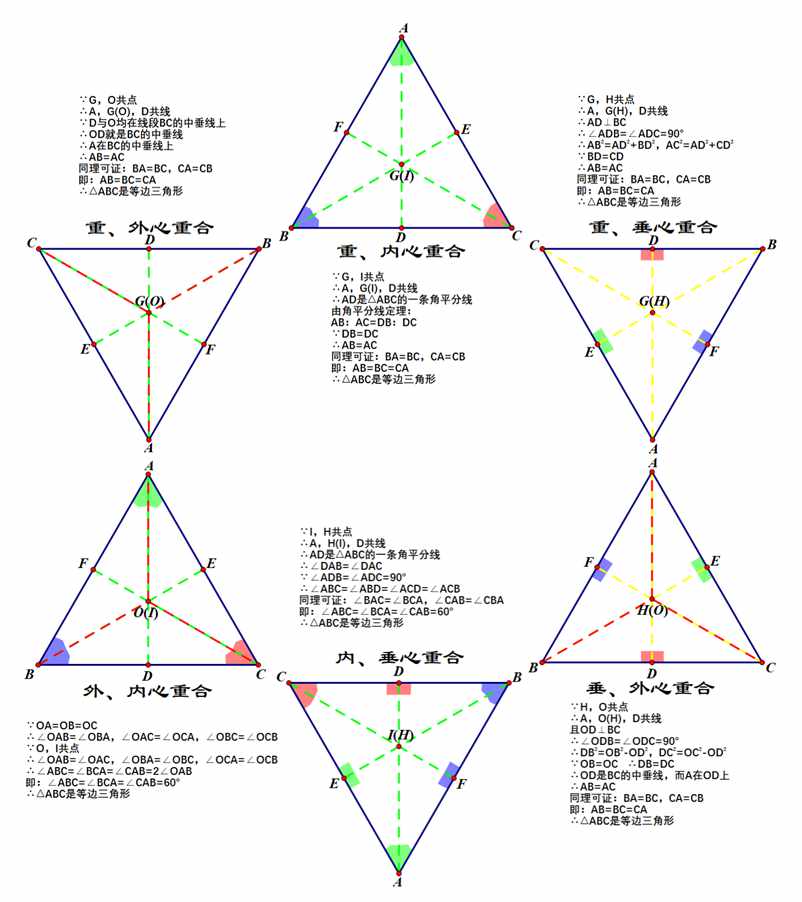
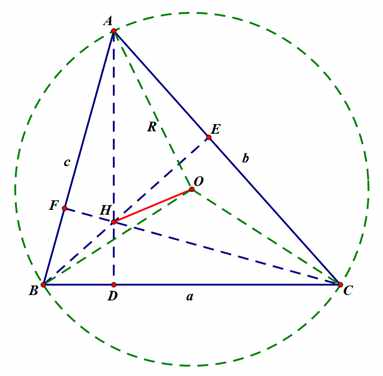
欧拉定理(夏普尔定理)——OI²=R²-2Rr:
这个欧拉成百上千的研究之一,描述了内外圆心距与两圆半径之间的关系,我在以前的专栏中曾详细地讨论过这个问题,今天就简单的了解一下吧:
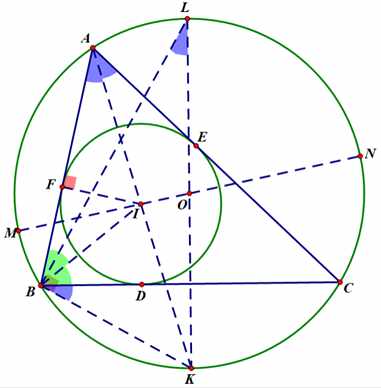
在此提供一个简单的证法
如图:延长角平分线AI,交⊙O于点K,过K作⊙O的直径KL,同时过点I,O作另一直径MN,连接IF,BK,BI
由四点共圆,易知:∠KBC=∠KAC=∠KAB(∠IAF)=∠KLB
同时:∠LBK=∠AFI=90°
∴△AFI~△LBK
∴AI:FI=LK:BK
即:AI·BK=FI·LK,其中,FI是△ABC内切圆半径r,LK是△ABC外接圆直径2R
∴AI·BK=2Rr
∵∠KBC=∠KAB,∠IBA=∠IBC
∴∠IBK=∠IBC+∠KBC=∠IBA+∠KAB=∠BIK
∴△KIB是等腰三角形,即:BK=IK
∴2Rr=AI·BK=AI·IK
由相交弦定理:AI·IK=MI·IN
而:MI·IN=(MO-IO)·(NO+IO)=(R-IO)·(R+IO)=R²-IO²
∴2Rr=R²-IO²
即:IO²=R²-2Rr
证毕
这就是双心距与两圆半径的关系公式,但是,我可不可以将两圆半径换成三角形三边长来表示呢?
让我们从三角形的面积公式入手吧:
三角形面积=底×高÷2
即:S△=ah/2
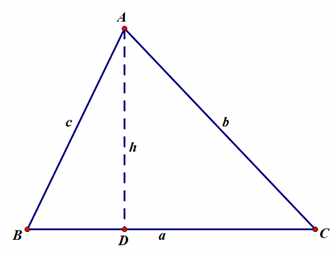
如果仅仅是这样,或许还发现不了什么,所以我们要稍稍改动一下:
在Rt△ADC中,有h/b=sin∠C
∴h=b·sin∠C
∴S△ABC=ah/2=ab/2·sin∠C
而由正弦定理,可得:sin∠C=c/2R
∴S△ABC=ab/2·sin∠C=abc/4R
∴R=abc/4S
同样,我们借助三角形面积公式与下图的分割方法:
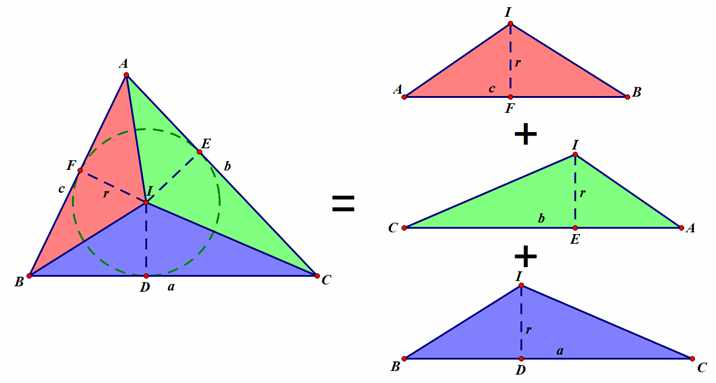
显然,由图可知:
S△ABC=S△ABI+S△AIC+S△IBC
=rc/2+rb/2+ra/2
=r(a+b+c)/2
∴r=2S/(a+b+c)
结合上面的:R=abc/4S,我们可以得到
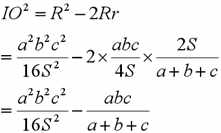
而S△ABC用三边长abc表示,这就要提到海伦公式了,证明的话到处都有,我就不再赘述了:
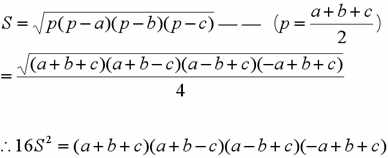
结合上面两式,得:
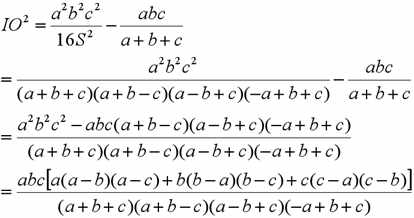
有点复杂,还是忽略它吧
好了,既然外心到内心的距离可以用三角形三边长计算而出,那么是否任意两心之间的距离都可以用三边长来表示?接下来就让我们来试着推一下吧:
OH:
由图所示
直接算太麻烦,让我们从向量入手,首先,我们可以利用这个式子:
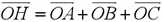
怎么证的?还记得我们证明欧拉线的作图吗?
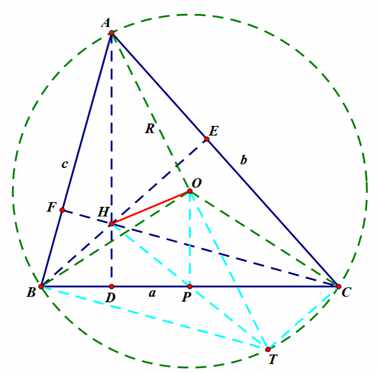
由图已知:四边形BHCT是平行四边形,P为HT中点,O为AT中点
∴OP为△TAH的中位线
∴OP∥AH且OP=AH/2,即:
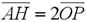
而显然:
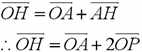
同样由图易知:
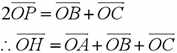
得证
有了上式,我们计算OH的长度就有了简单的算法:
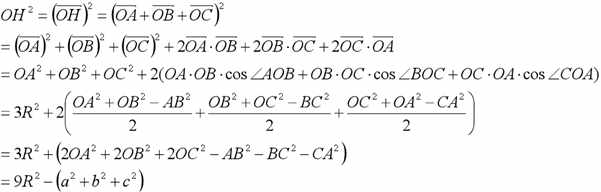
看,就这么简单
OG、GH:
有了前面的欧拉线做的铺垫,相信这两条线段长并不怎么难求吧。
由之前所得:O,G,H三点共线,且OG:GH=1:2
∴OG:OH=1:3,GH:OH=2:3
∴OG²=OH²/9=R²-(a²+b²+c²)/9
GH²=4OH²/9=4R²-4(a²+b²+c²)/9
之后再将R²由a,b,c表示就行了,这里我就不写出来了
IH、IG:
这两条线段算是三角形里最难表示了的吧,毕竟我现在也只能通过“暴力计算法”来求出它们的表达式:
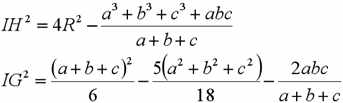
当然,如果大家有什么更加简单的证明方法,就在评论区里讨论讨论吧。
最后,我还有一个问题要大家来解决一下,这个问题是我在“无聊”的时候想到的,具体问题如下:
能否在仅知道某三角形四心位置的条件下,用尺规作图还原该三角形?
通过上面的铺垫,我们可以知道,在已知四心位置的条件下,就是已知下面六条关于三角形三边长的方程,最后解出答案即可:
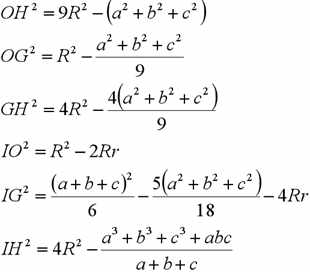
R与r可以转化成用a,b,c表达的式子,这里就不麻烦了
当然,仅仅是解方程的话,理论上是可以解得a,b,c并得出公式解,毕竟通分化简后的方程最高次也不超过4次,可解,并且是唯一解。但是,如果是需要用尺规作图来实现的话,就可能不存在了,因为尺规能够完成的运算只有:加,减,乘,除及开方五种罢了,除此之外连最简单的“³√2”都做不出来(倍立方问题)。
同时,看过我上面发的专栏后,大家应该知道了,在仅知道外心与内心的情况下,我们可以做出无数种三角形,甚至将两圆半径确定的条件下,依然有无数种三角形满足条件:
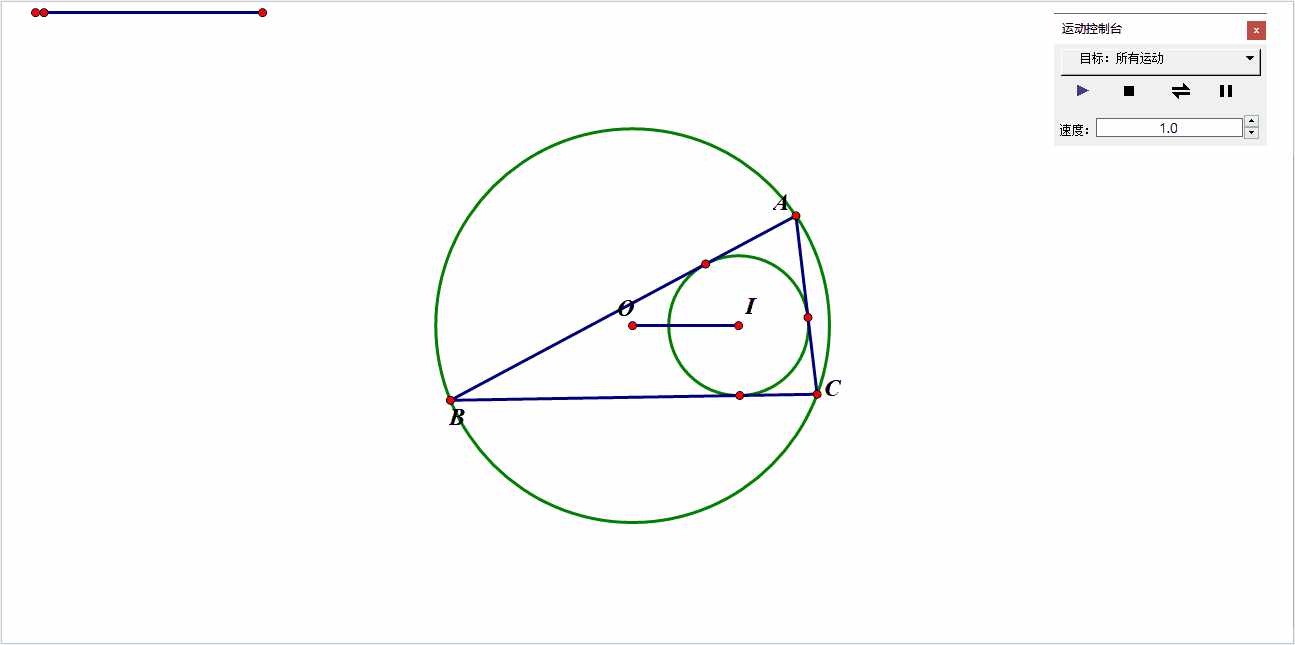
已知I与O虽知I与O,仍有无数种
同样,仅知道外心与垂心,也有无数种三角形:
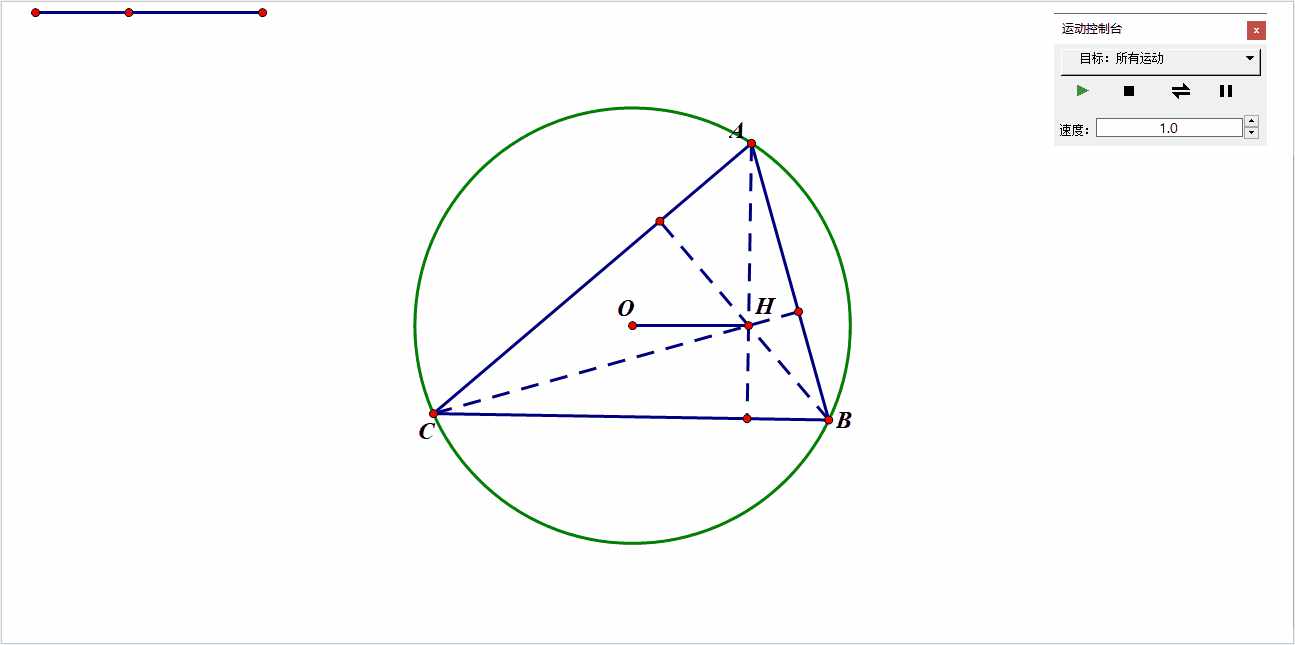
已知O和H
但有趣的是,如果同时给出O,I,H时,这个三角形就被确定下来了,如下图:
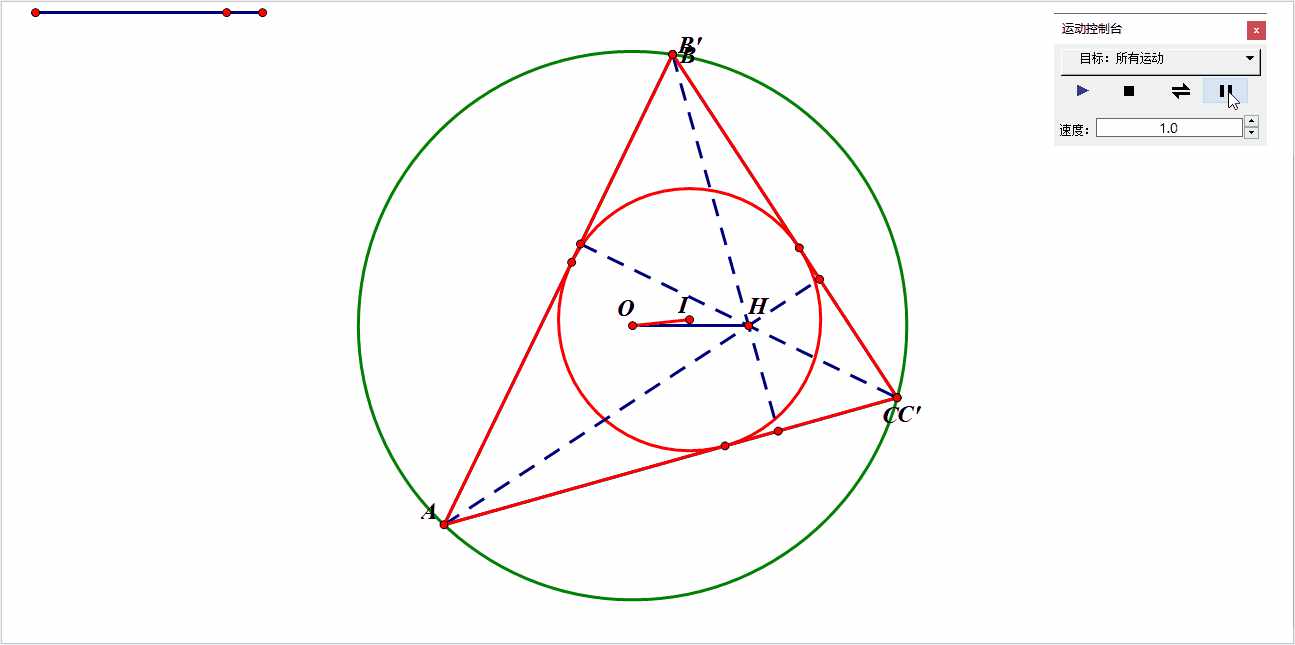
别看其中有几处似乎重合,那只是非常近似罢了
而且,大家应该注意到,我这里没有提到重心G,毕竟由于欧拉线的存在,使我们可以只由O,G,H中的任意两点得出第三点的位置。所以,所谓的四心,只要知道三心的位置就够了,当然,其中必须要有内心。但是,并不是所有四点组都可以满足做为三角形的四心,首先的三点共线是必须的,并且其中一点要在两点连线段的三分之一的位置处,同时内心也有一定的范围,大致在重心与垂心之间,证明就交给大家吧。
那么,以上就是题目了,大家有没有什么想法啊?毕竟用尺规作图解题可不容易啊。我也只找到一种特殊三角形的做出方法——等腰三角形。但一般三角形则没有什么眉目,期待大家的答案吧。
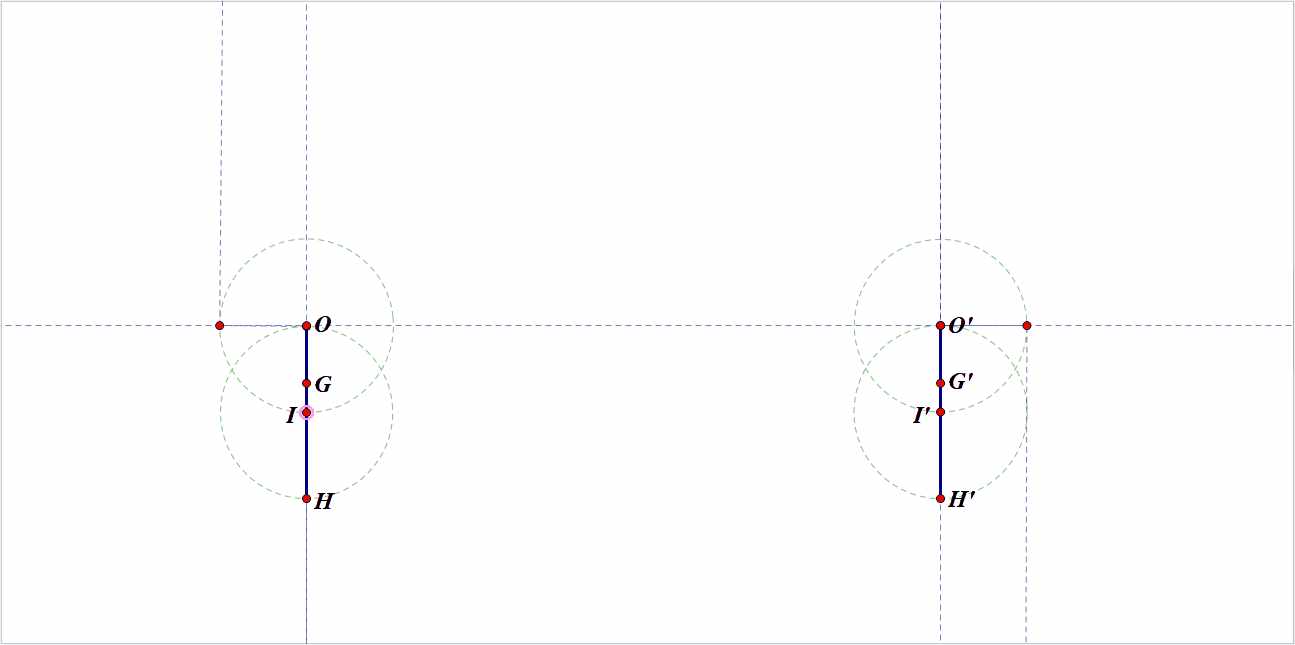
分两种情况哦,I在OH中点下与I在OH中点和G之间
做法的证明很简单哦,思路是首先通过已知的四点找出外接圆半径,同时确定三角形的顶点,然后再通过垂心确定三角形的底边,这样,等腰三角形就做出来了。最重要的是证明:在等腰三角形中,有│OI - IH│=R-2r,再结合OI²=R²-2Rr,就可以得到外接圆半径R了。


证毕
最后的最后,总结一下吧,稍稍没注意,又写多了(但还是有“些许”东西没写到啊),不过相比于学校里学的,我还是加了点新东西的嘛。当然,我“不太期望”大家能把我最后这个疑问给解决,但是,想一想总没有坏处是吧。算了,你们看着烧脑,我开心就好(ಡωಡ)hiahiahia
以上就是(三角形四心随想 (三角形四心与向量的关系))全部内容,收藏起来下次访问不迷路!