彭罗斯镶嵌与一维序列

彭罗斯镶嵌与一维序列罗杰·彭罗斯，英国数学物理学家、牛津大学数学系名誉教授，最近因为对黑洞奇点出色的研究，获得2020年诺贝尔物理学奖。而在之前，他的一项数学研究成果为

彭罗斯镶嵌与一维序列

罗杰·彭罗斯，英国数学物理学家、牛津大学数学系名誉教授，最近因为对黑洞奇点出色的研究，获得2020年诺贝尔物理学奖。而在之前，他的一项数学研究成果为一项诺贝尔化学奖的相关研究——准晶体——奠定了坚实的数学基础。

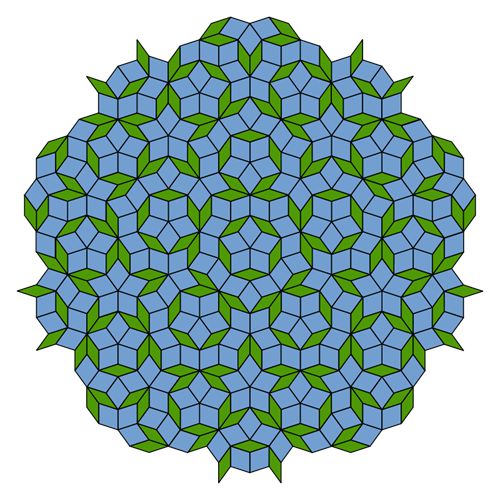
彭罗斯研究的是平面密铺问题，而他得到的研究成果是：彭罗斯镶嵌（Penrose tiling，或译作彭罗斯瓷砖、彭罗斯密铺等，tiling有名词瓷砖和动词铺瓷砖两种含义）

从五个方向上可以看到五个蝙蝠侠面具hhhhhhh

中科院物理所的科普中有这么一项描述：

1974年，物理学家罗杰·彭罗斯（Roger Penrose）以正五边形为基础，设计出了一种惊人的瓷砖图案。他发现仅通过两种不同的形状，就可以构造出一个能实现五重对称，并能无限延续下去且不会自我重复的图案。也就是说用两种形状的瓷砖进行平铺最终会得到非周期性的图案。

出处：

为了易于理解，科普语言有时候会牺牲一点点准确度。这里的不会自我重复，其实有可能令读者产生错误的理解。爱思考的读者可能会感到奇怪，看起来明明会重复啊？

用最准确的语言来说，我们只能把这里的不会自我重复，理解为没有周期性。没有周期性可不一定不会重复。

什么叫周期性？我们不是毕导，我们在初中二年级才学到三角函数。我们说三角函数是周期函数，一个等价（而不太严谨）的叙述是：我们平移三角函数的图像一段（长度为某个周期的）距离，会和原来的函数图像重合。二维图像的密铺的周期性也可以这样描述：三角形、正方形、正六边形、任意四边形等周期性的密铺，可以向某个方向平移一段距离，得到的新图像和原图像完全重合。

而彭罗斯发现的非周期密铺就。。。就是非周期。

强迫症患者福音

这个无穷大的图案一直不会重复【官方双语】【Veritasium真理元素】

那为什么说没有周期性可不一定不会重复呢？

因为确实会重复：

The pattern represented by every finite patch of tiles in a Penrose tiling occurs infinitely many times throughout the tiling. （彭罗斯镶嵌中每个有限拼贴片所代表的图案在整个图案中无限次出现。）

周期性密铺的图案会无限次出现是显而易见的，但是这里明明是非周期，也出现无限次，就。。。喵啊！

1. 一维序列

二维图案的密铺太难了，任意图案都能出现无限次，这个性质很妙，但是太难证明了。我们可以讨论讨论一维的密铺。

（emmmmmmmm那不就是线段铺在数轴上了吗）

对的就是线段。显然，如果我们只有一种线段，首尾相连铺在数轴上，那么肯定是周期的。所以，我们至少需要两种不同长度的线段。如果我们把两种线段分别取外号：0和1，那么这个密铺可以写成左右无限延伸的01序列：

。。。。。。。。。。。。011010100010001011。。。。。。。。。。。。

大概是这个样子。我们的问题的变成了：

是否存在这样一个非周期01序列，其中任意长度的一段序列的排列方式，都会在整个序列中出现无数次？

（这个叙述非常不严谨，读者可以自行尝试一下如何严谨地表达这个问题）

乍一看这个问题好像很难的样子，但是知道钱珀瑙恩数(Champernowne)的读者，可能已经想到了一种方法。

钱珀瑙恩数的构造方法很容易理解：0.1234567891011121314151617。。。把自然数连起来写就完事了。

我们可以仿照这一点，写出二进制版的序列：0, 1, 10, 11, 100, 101, 110, 111。。。然后去掉逗号即可。当然这个序列只向一个方向延伸，我们可以对称地往左边同样一直写下去。这样一来，我们成功得到了一个符合我们前面所述的序列，而且还具有轴对称性。