(快乐数学)射影定理
(快乐数学)射影定理
射影定理。
比较妙的是,在老教材选修4-1有一个射影定理(姑且管它叫直角三角形的射影定理吧)

而我想说的是另一个射影定理。
那就先说说直角三角形的射影定理吧。
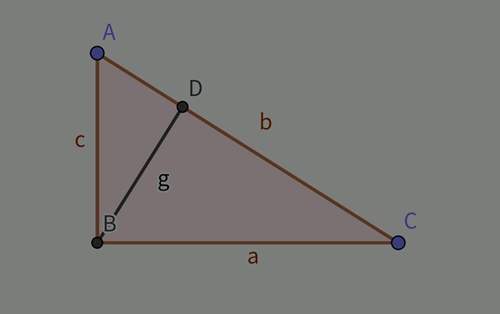
如图,在直角三角形ABC中,BD为斜边上的高。
而△ABD∽△CBD∽△ABC
∴AB²=AC·AD
BC²=AC·CD
BD²=AD·CD
这便是直角三角形的射影定理。
这个定理在初中用用还是不错的。
高中emmm
极个别情况也能用到。
除此之外呢还有一个射影定理
在任意的△ABC中,
A+B=π-C
于是
sin(A+B)=sin(π-C)
再用诱导公式
得到
sin(A+B)=sinC
展开得到
sinAcosB+cosAsinB=sinC
再用正弦定理,角化边得到
c=acosB+bcosA
这便是射影定理了。
从几何角度看
acosB是a在c上的射影
所以它叫做射影定理。
那么这个定理有什么用呢?
其实没什么用,基本遇不到。
但是遇到了会很爽。
比如说

直接用射影定理得到
2bcosB=b
2cosB=1
cosB=0.5
B=60°
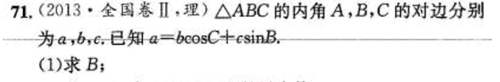
把a换掉
得到sinB=cosB
得到B=45°

提出sinB,用射影定理
得到bsinB=0.5b
那么sinB=0.5
再用大边对大角
B=30°
爽就完了。
以上就是((快乐数学)射影定理)全部内容,收藏起来下次访问不迷路!
86%的人还看了:(干货)如何写文献综述?最详细的解释